マイコン/デジタル回路
電子工作関連の記事です。アンプ回路はこちら。
電子工作関連の記事です。アンプ回路はこちら。


今日郵便局に行ったら、かごに入ってティッシュが配られていました。まだまだ使えるティッシュなのにこういう配り方は勿体ない。
これが大人の事情って奴ですね。
※この記事で解説していることは半分誤っています。ダイオードの特性よりもオペアンプのスルーレートが問題であり、FETでバッファすることはスルーレート改善に効果的です。
ピーク検出回路などではダイオードが整流のために使われます。実際のダイオードは理想的ではないため簡単には行きません。100kHz の sin波 を検出することを考えてみます。
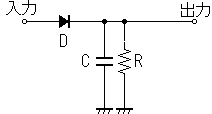
まずは誰もが思いつく簡単なピークホールド回路です。回路図中のRは放電用抵抗です。CRで時定数となりますが100kΩ~1MΩ、Cは0.01uF~1uFなどを使用します。例えば、100kΩ、0.01uFならば時定数は100k*0.01u=1msとなります。
「入力電圧>出力電圧」(コンデンサに充電されている電圧)のとき、ダイオードの電流が流れコンデンサが充電され「入力電圧=出力電圧」となるとダイオードがオフになって最大電圧を計ることができるという回路です。
この回路がうまく行かないことは多くの人が気づくと思います。ダイオードには順方向電圧というものがあり、約0.7Vの電圧降下が起こります。逆に言えば「入力電圧>出力電圧+0.7V」でないとダイオードに電流が流れませんので、0.7Vより小さな信号のピークを計測することができません。
またダイオードには電流によって順方向電圧が非線形に変化する特性がありますので、これもまた正確な測定には向きません(下図は1N4188の電流電圧特性)。

ダイオードの順方向電圧や非線形特性の問題をクリアするための典型的なピーク検出回路です。FET入力のオペアンプ(コンパレータでも可)を使用します。*1
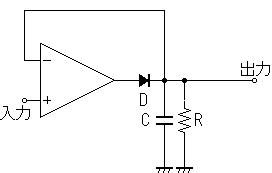
出力電圧より入力電圧が高い場合、電圧差に関わらずオペアンプは+V(電源)に近い電圧を出し続けますので勢いよくコンデンサが充電されます。そして入力電圧より出力電圧が高くなれば、オペアンプは-Vを出力しダイオードに電流が遮断さることによって、ピーク時の電圧がコンデンサにより保持されます。
実際この回路は機能的に動きます。オペアンプ LF356N、C=0.33uF、R=220kΩ、D=1S1588(小信号高速スイッチング用)、電源±15Vで実際に出力電圧を計測してみましょう。DCは直流、sinは0-p電圧です。
| 入力電圧 | DC | sin 100kHz |
|---|---|---|
| 50mV | 35.0mV | -0.2mV |
| 100mV | 71.1mV | -0.4mV |
| 200mV | 170.0mV | -0.3mV |
| 300mV | 268.6mV | 45.7mV |
| 400mV | 367.7mV | 117.3mV |
| 500mV | 466.2mV | 192.6mV |
| 700mV | 664.1mV | 349.2mV |
| 1V | 955.6mV | 594.1mV |
| 2V | 1.944V | 1.439V |
| 3V | 2.932V | 2.290V |
| 5V | 4.906V | 3.969V |
DCならばきちんと計れていますが、100kHzのsin波はまともに計測できているとは言い難い状況です。200mV以下のsin波に至っては全く計測できないことになります。
DCだと計測できるのに、高々100kHzのsin波だとまともに計測できない。しかもDCの方は線形な変化をするのに対し、sin波の方は非線形な入出力特性を持っています。一体何が起こっているのでしょうか?
ダイオードにはリカバリー特性というものがあります。PN接合面がONになった状態から、逆電圧が掛かりダイオードがOFFになるまでの時間のことをリカバリタイムと言います。詳細はリンク先を参照して頂きたいのですが、PN半導体に存在する電子やホールが移動することによってダイオードはオフになります。実はこの移動時間というのは速くありません。それは電子などの信号の伝達時間と違い、物理的な移動時間だからです。
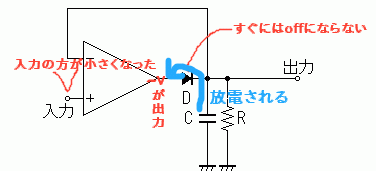
よって、入力電圧が現在の保持電圧を下回ってもすぐにはオフにならず、せっかく溜まっていた電荷が-Vにめがけて流れ出してしまいます。よって電圧が下がってしまうのです。微小信号では、コンデンサにたまる電荷 Q=CV の V が少ないので素早く放電されてしまうどころか、マイナスの電荷をため込んでしまうというわけです(電源電圧 -V=-15V は、充電されている電圧 100mV などに比べ非常に大きいため簡単に流れ出します)。
一般に、周波数が高ければ高いほど、検出電圧が低ければ低いほど、その測定は困難になります。
まず思いつくのがダイオードをFRD(ファーストリカバリダイオード)やSBD(ショットキーバリアダイオード)などのリカバリ時間短いものに変更することでしょう。
試しにSBDで実験すると、まともに計測できなくなりました。SBDの特性として忘れてはいけなのは漏れ電流が大きいことです。漏れ電流によりそのまま放電されるため整流(波形整形)すらできなくなり、sin波がほぼそのまま出力されます。そもそも小信号高速スイッチング用である1S1588の逆回復時間は4ns程度でして、FRDよりよっぽど速いくらいです*2。
そもそもの問題はダイオードの前に -V が出力されてしまうことで、この部分をクリアすれば(完全には解決しないにしろ)かなり良くなるだろうと考えました。
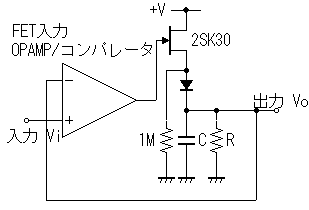
負電圧-Vを出力せず、FETでスイッチしてしまうという回路です。+Vとハイインピーダンス出力になります。実際にはわずかに電圧がゲートからドレイン側に漏れるため、すこしだけ電位が下がってしまいます。
FETの代わりにバイポーラトランジスタを使うことはできません。2SC1815で試しましたがほとんど改善しませんでした。考えてみれば単純な話で、バイポーラトランジスタのベースエミッタ間は単なるダイオードですから、結局同じ問題に当たるわけです。
計測結果をここに示します。その他条件は上と一緒です。
| 入力電圧 | 出力電圧 | ダイオードなし回路 |
|---|---|---|
| 50mV | 28mV | 40mV |
| 100mV | 61mV | 87mV |
| 200mV | 128mV | 183mV |
| 300mV | 194mV | 280mV |
| 400mV | 260mV | 378mV |
| 500mV | 325mV | 475mV |
| 700mV | 458mV | 671mV |
| 1V | 658mV | 966mV |
| 2V | 1.505V | 1.97V |
| 3V | 2.362V | 2.96V |
| 5V | 4.060V | 4.95V |
小さい電圧も検出できるようになりましたが、結局ダイオード等の非線形性からは逃れられず、入出力電圧が非線形になっています*3。とりあえず、この値をADCで取り込んで非線形補正をかけることにしました。
ネットを調べていると、こちらのダイオードを使わないピーク検出回路が良さそうな感じです。コンパレータがないためLF356N+2SC1815で同じ動作の回路*4をつくって検証したところ上の表「ダイオードなし回路」のようになりました。ほとんど線形で、かなり特性が良いです*5。
長年理解するのを拒否していたFFTとここ何週間か格闘しています。楽々とアルゴリズムを導出・実装できる人はいいのでしょうが、FFTのようなアルゴリズムをきちんと理解して実装するのは思うほど容易ではありません。既に導出されたアルゴリズム(や雛形サンプル)を何も考えず実装すれば簡単ですが、そういうことが生理的にできない場合、改良とかを考え出して簡単には実装できなくなるんですよね。
前置きはともかく、今日やっと実数専用のFFT/IFFTが作成できました。実数専用にすることで理論的には通常のFFTの半分の時間で処理できます。
見ての通り、実数FFTの対称性を利用したものすごく面倒くさく複雑な作りになっているんですが、有名なFFTの概略と設計法のソースと速度比較をしたら倍近く遅い……。64K点、double型、VIA C3 500MHzで動作させて、自作が100ms、リンク先のソースが60ms。
いかに細かい最適化をしても実装アルゴリズムの時点で差があると非常に大きいですね……。あとでアルゴリズムの差を検証予定。
大浦氏のFFTソース(fft4g.c)解読メモ。つまりリバースエンジニアリングです。
| cdft() | 複素数FFT/IFFT。データサイズは N/2 |
| rdft() | 実数FFT/IFFT。内部的に複素FFTを呼び出し |
| makewt() | sin/cosテーブルを w[] に格納(ただし格納位置はビット反転) |
| makect() | cosテーブルを w[nw~] に格納(ただし格納位置はビット反転) |
| bitrv2() | ビット反転を実行 |
| bitrv2conj() | ビット反転しつつ、読込データの複素共役を取る |
| cftfsub() | 複素IFFT(f=forward, 回転子が正であるという意味) |
| cftbsub() | 複素FFT(b=backward, 回転子が負であるという意味) |
| rftfsub() | 実数IFFT |
| rftbsub() | 実数FFT |
なんだけども、複素共役を考えると
つまり前処理と後処理としてデータの複素共役を取ってあげれば、同じFFTルーチンを使い回すことができる(効率を考えて、初段部分と終段部分だけ個別特別に実装すれば、中段部分は使い回せる)。
やっとこのプログラムの要が理解出来ました。
先にデータをスクランブルして(並べ替えて)いるため「時間間引きFFT」に見えますが、実際には周波数間引きFFTです。sin/cosテーブルもわざわざスクランブル位置に格納しています。
こうすることでFFT実行時のデータアクセスをシーケンシャルに行え*2、それが功を奏して実行速度が飛躍的に速くなっています。またsin/cosテーブル、偶数番地に cos、奇数番地に sin を格納し、全体としても π/2 しか用意しないことで、データアクセス量を減らしキャッシュが効きやすくなっています。
256点の複素FFTを実行させたときの、cos/sinテーブル参照位置およびデータ参照位置は次のようになります。
call cftmdl(512, 8)
k1=1 (0.923880,0.382683), k2=2 (0.707107,0.707107)
32 36 40 44
33 37 41 45
34 38 42 46
35 39 43 47
k1=2 (0.980785,0.195090), k2=4 (0.923880,0.382683)
64 68 72 76
65 69 73 77
66 70 74 78
67 71 75 79
k1=3 (0.831470,0.555570), k2=6 (0.382683,0.923880)
96 100 104 108
97 101 105 109
98 102 106 110
99 103 107 111
k1=4 (0.995185,0.098017), k2=8 (0.980785,0.195090)
128 132 136 140
129 133 137 141
130 134 138 142
131 135 139 143
k1=5 (0.881921,0.471397), k2=10 (0.555570,0.831470)
160 164 168 172
161 165 169 173
162 166 170 174
163 167 171 175
k1=6 (0.956940,0.290285), k2=12 (0.831470,0.555570)
192 196 200 204
193 197 201 205
194 198 202 206
195 199 203 207
k1=7 (0.773010,0.634393), k2=14 (0.195090,0.980785)
224 228 232 236
225 229 233 237
226 230 234 238
227 231 235 239
call cftmdl(512, 32)
k1=1 (0.923880,0.382683), k2=2 (0.707107,0.707107)
128 144 160 176
129 145 161 177
(中略)
142 158 174 190
143 159 175 191
ほんと、この実装はすごいなぁ。
verilog HDLを勉強がてら遊んでいるのですが、つまずいています。
よくあるサンプルですが、
input [1:0] SW; reg [3:0] counter; always @(posedge SW[0] or posedge SW[1]) begin if (SW[1] == 1) // reset counter <= 0; else counter <= counter + 1; end end
と書くと正しく動作します。ですが、
always @(posedge SW[0] or posedge SW[1]) begin if (SW[0] == 1) counter <= counter + 1; else counter <= 0; end end
と書くとまともに動作しません。SW[0]を押したとき、値が不定値になります。またSW[0]を押している間、counterの値が随時変化し全く定まりません。どなたかお助け。
シミュレーションだとどちらも正常に動きます。なんかバグ(不具合?)っぽい予感がヒシヒシと(汗)