FFTとは? ~本当は正しくないFFTの周波数特性~
エンジニアや理工系の人と話をしていると、FFT=周波数特性と勘違いしている人が大勢います。それも絶対に正しいと思っている人が居るんだけどそれは大間違いです。
なるべく数式を使わずに簡単にFFTとは何であるのかを解説します。
フーリエ変換とは
フーリエ変換=FFTと思っている人も多いのですが、これも間違い。
フーリエ変換とは
無限に続く任意の連続信号(1次元)を、無限の周波数までのsin波とcos波の重ねあわせとして表現できる
ことを利用してある任意の信号を、sin波とcos波の重ね合わせ(積分)として表現することをフーリエ変換と言います。
元の信号をf(t)、変換後の信号をg(x)とすれば次のようになります。*1
\displaystyle f(t) = \int_{-\infty}^{\infty}g(x)(\cos(2\pi xt)+j\sin(2\pi xt))dx
フーリエ級数展開とは
フーリエ変換とフーリエ級数展開を混同している人も多いと思います。フーリエ級数展開とは、
ある有限の長さの繰り返し連続信号(1次元)を1~無限までのsinとcosの級数として表したもの
です。
一般には(無限の長さを持つ)周期関数で定義されていますが、「ある有限の長さ」の信号を繰り返すことで「無限の長さを持つ周期関数」が得られることから、「有限の長さの信号」が本質であることを捉えておくと良いと思います。
元の信号をf(t)、級数展開後の係数を a(k), b(k) で表すと次のようになります。*2
\displaystyle f(t) = \frac{a(0)}{2}+\sum_{k=1}^{\infty} a(k)\cos(t)+b(k)\sin(t)
フーリエ変換やフーリエ級数展開の特徴
フーリエ変換は無限に続く連続信号に対するもので、フーリエ級数展開は有限長の連続信号に対するものです。どちらも、sin波とcos波の加算として表現されることから、その信号の持つ周波数ごとの信号の強さを知ることができます。
ですが、ここに問題があり、コンピューターが無限に続くものを扱えないのは当然としても、そもそも連続信号を扱うことができません。
標本化と量子化
連続について大雑把に解説すると1秒間に無限個のデータがあるということです。こんなものコンピューターで扱えるわけがありません。ですので、コンピューター上で信号を扱う場合は1秒間に適当な個数だけデータを抽出して処理します。これが標本化です。サンプリングとも言い1秒間に取り込むデータの数をサンプリング周波数といいます。サンプリング周波数48kHzということは、1秒あたり48000個のデータを取り込むということです。
さてこれでコンピュータで処理できます、と解説している所も多いのですが、これも間違い。取り込んだ1つ1つのデータは信号の大きさを持っています。電圧ならば0.2Vとか0.5Vとか1Vとかです。例えば、最低で0V、最大で1Vまでということが分かっていたとして、0V~1Vまでの間で取りうる値というのは果たして何個あるかと言うと、これも無限個あります*3。
これを適当な個数に区切って、それぞれ値で近似することを量子化といいます。10個で量子化すれば0.1V刻みになり、0.11Vを0.1V、0.26Vを0.3Vにという具合に丸めます。量子化ビット数が8bitなら256個、16bitなら65536個、24bitなら1677万個に区切るという意味になります。
以後は量子化されたデータでも、量子化されてないデータでも全く同じように処理できるため量子化の話は出てきませんが、コンピューターで処理する限りは量子化されたデータなのだと思っておいてください。
このような処理を行うことを総じて離散化といいます。
時間軸の離散化=標本化(サンプリング)
振幅軸の離散化=量子化
離散フーリエ変換(DFT)とは
フーリエ変換は無限に続く連続信号に対してのものでしたが、コンピュータで扱う離散化された信号に対して同じようなものを考えれば、コンピュータ上で信号の周波数特性のようなものが得られそうです。
この考えで「離散データに対するフーリエ変換のようなもの」を考え、これを離散フーリエ変換と言います。正確には、連続信号を離散化したようにフーリエ変換を離散化したものなのです。
離散フーリエ変換とは、(有限である)N個のデータを、N個の周波数のsin波とcos波の信号の大きさ*4に変換することです。
元のN個のデータからなる信号をf(n)、変換後の信号をa(k),b(k)とすれば次のようになります。
\displaystyle f(n) = \sum_{k=0}^{N} a(k)\cos\frac{2\pi kn}{N}+jb(k) \sin\frac{2\pi kn}{N}
このようにフーリエ変換という名前を持ちながら、フーリエ級数ととても似た式をしています。後で解説するとおり、実際にフーリエ級数と似た性質を持っています。
高速フーリエ変換(FFT)とは
離散フーリエ変換(DFT)をコンピュータで計算するとき高速に処理するためのアルゴリズムの名前です。理論や手法の名前ではなく、高速に処理するための姑息な手段に対する名前です。*5
ただ、事実上、コンピュータ上でフーリエ変換といえばFFTというほど有名で有力な手段であるためFFTが離散フーリエ変換の代名詞となっています。理論上はDFTと何一つ違いがありません。
FFT(DFT)の本質
FFTが扱うデータは有限です。一般に「4096点や8192点などの要素数*6」を使用しますが、ここにFFTの本質があります。
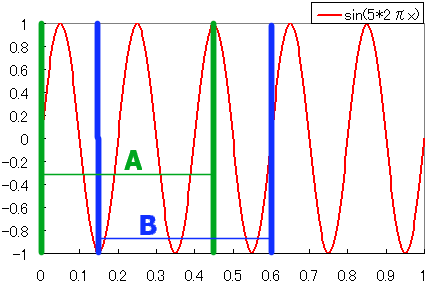
図は5Hzの信号で区間Aも区間Bも同じ幅、同じ点数です。これを4096点FFTしたらどちらもキレイに5Hzだけ大きさのある周波数特性が表示されるでしょうか? 残念ながらそうなることは決してありません。
まず10Hzや15Hz、20Hzなどの高調波信号成分も表示されます。これは区間の端で信号がぶち切れているためです。またAとBで表示される周波数特性も異なります*7。同じ5Hzの信号を同じように処理しているのに!です。
では次の信号ならどうでしょう?
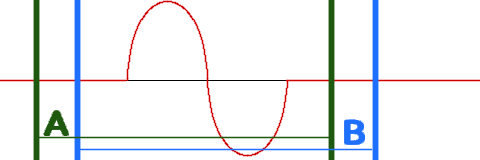
今度は端が切れていませんが、これでもAとBで表示される周波数特性は異なるのです*8。FFTは切り出す位置(これを窓という)がものすごく重要で、信号の切り出し方ひとつで得られる周波数特性がコロコロ変わります。
もうひとつ、5Hzの信号をFFTしても5Hzのみのピークが得られない原因があります。それは、フーリエ変換してもほとんどの場合5Hzというピンポイントの周波数値を持たないのです。例えば48kHzでサンプリングされた1kHzの信号データを4096点FFTしたとします。このとき、4096/48k=85.33msで逆数は 11.71875Hz なので、得られる周波数の点は 11.71875Hz の倍数(0~2047倍まで)なのです。ですので1kHzの信号だけを処理したとしても、信号エネルギーは 996.09375Hz と 1007.8125Hz に分散されて表示されます。*9
どうしてFFTは正しくないのか
FFTで得られる周波数特性がいかに正しくないか多少は実感して頂けたと思いますが、どうしてこのような現象が起こるのでしょうか。
FFTで正しい周波数特性が得られるのはある条件が満たされたときだけです。それは信号全体がFFTの処理対象として切り出したデータの繰り返しになっていることです。別の言い方をすれば、FFTとは有限の長さの信号を全体がその繰り返し信号であると思って周波数特性を求めています。
実はFFTは周波数スペクトル測定方法ではなく周波数スペクトル推定方法に分類されます。FFTで表示される周波数特性(スペクトル)はあくまで推定に過ぎないのです。窓関数という言葉を聞いたことがあるかと思いますが、端で信号が切れることに代表される問題を誤魔化すため、色々な特性を持った窓関数が考案されています。
このようにFFTは切り出した有限の長さの信号をその部分が永遠に繰り返すもの(周期信号)とみなして処理していますので、性質がフーリエ級数と非常に良く似ていて定義式も酷似しています。
(おまけ)スペクトル推定法と基底変換
ほかに、ARMAという(もしくは単独でARやMA)といったスペクトル推定法があります。ARスペクトル推定法というものを使うと、窓関数でぶった切ることなしにスペクトルを推定することができます。これはこれで欠点もありますが、考え方がアナログ回路で言うところのLCRフィルタに近いのでFFTよりも実感に近いようにも感じます。
以前IIRフィルタによるsin波生成の話を書きましたが、信号フィルタとして使われるIIRやFIRフィルタは、ARやMAと深い関わりがあり、本質的にはこれらは同じものです。これもあまり知られてませんね。
最後にちょっと難しい話をしますが、フーリエ変換もFFTもやっていることはただの基底変換です*10。基底変換というのはざっくりと言うと視点を変えるということで、例えばぬいぐるみを目の前において、これを斜めから見れば基底変換したことになります。同じものでも見る角度を変えることで見方が変わるという現象を巧みに利用しています。ちなみに色の表現であるRGBをYUVに変換するのも基底変換です。
(おまけ2)フーリエ変換の存在についての補足
DFTやFFTにはまったく関係のない話です*11。安易に読んでも混乱するだけかも。
フーリエ変換の説明で「任意の連続信号をフーリエ変換できる」と書きましたが、より厳密にはフーリエ変換できない連続信号も存在します。例えば、
\displaystyle f(t)=t ※t→∞で発散
\displaystyle f(t)=\frac{1}{t} ※t=0で発散
のように発散してしまう関数は扱うことができません(フーリエ変換が存在しません)。
また不連続点と言い、関数がぶち切れてる*12点ではフーリエ変換した値は一致しませんし、このような不連続点が番号付けできない程度に無限に*13存在するときはフーリエ変換することができません。しかしそのような関数はそもそも普通に考えてる範囲では出てきません。
例えば
\displaystyle f(t)=0(t!=整数), \displaystyle f(t)=1 (t=整数)
という関数は(加算無限個ある)整数において不連続となる関数ですが、こんな関数でもフーリエ変換できます。*14
