アナログ回路とアナログフィルタの超入門
※本稿はC76でのstrvさんのサークル同人誌への寄稿原稿を元にして記述しています。文中のコラムは一部省略しました。
寄稿原稿のpdf版 : strv-c76-nabe.pdf
ヘッドホンアンプ等のオーディオ回路を念頭に、中学生レベルの知識から出発して、最後に簡単なローパスフィルタを設計することを目標に「ざっくり」解説してみたいと思います。初歩の回路記号の解説は省略するので、適当な本やサイトを参照してください。
オームの法則
オームの法則は電圧と電流の関係を示すもっとも基本的なものです。
電圧=電流×抵抗値
電圧はV、電流はI、抵抗はRと書くので、この式は次のようになります。
V=IR
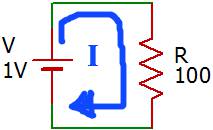
図は1Vの電圧が100Ωの抵抗にかかっている様子を示しています。I=V/Rですので、1V/100Ω=0.01Aの電流が流れている計算になります。回路の計算練習ならA(アンペア)のままで良いのですが、実用上はAという単位は大きすぎます。普通は補助単位m(ミリ)を使用して0.01Aではなく10mAと書きます。
電圧の捉え方
オームの法則から回路を学ぼうとするとき、最初につまずくのはGND(グランド)の捉え方です。
先ほどの回路をGNDを使って左図のように書き直してみます。
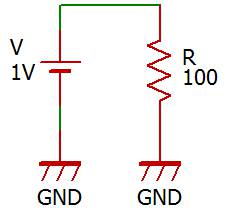
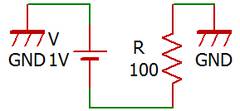
GND同士は接続されているとみなされるので、この回路は先ほどの回路と全く同じものです。では右図の回路はどうでしょうか。普通左図のようには書きますが、右図のようには書きません。電源が1つならば低い方を基準にします。
GNDとは0V地点であり基準です。
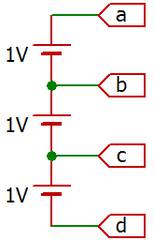
この意味を理解するために電源が複数ある場合を考えます。次の図は電池が3つ直列に並んでいる回路図です。
(d)をGNDとすると、(a)は3V、(b)は2V、(c)は1Vになります。(d)はGNDで基準ですので0Vです。(b)をGNDとすると(a)は1V、(c)は-1V、(d)は-2Vとなります。
回路上意味がないのにどうしてGNDという基準を決めるのでしょう。
話は変わりますが、あなたはどこに住んでいますか。平野部? 海岸線? 山間部? 今居る場所の標高がどれくらいか分かりますか。その場所の高さを示す標高は、海抜とも言います。海抜とは海水面の高さを基準としたその場所の高さです。高さというのは相対的なものなので、基準をどこかに決めないと富士山もエベレストも高さを比べることができません。もし東京タワーやピラミッドといった建造物の高さを比べたければ、海面ではなく「その場所の地面」を基準にし、絵に並べるなら地面(基準)を揃えるのが普通です。
電圧も高さと同じように相対的なものです。基準をどこかに決めないと、回路と回路を接続することができません。CDプレイヤーとアンプ繋ぐことができるのは、GNDという基準があり、GNDという基準に対してどのような信号をやりとりするか決まっているからなのです。
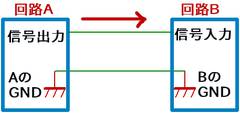
ですから、信号をやり取りするときは最低2本以上接続し、信号線と一緒にGND同士を接続して基準を共通にするのです。
分圧
信号は普通電圧で表現されます。単に信号と言ったときは電圧だと思ってください。
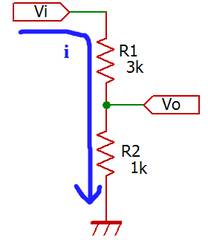
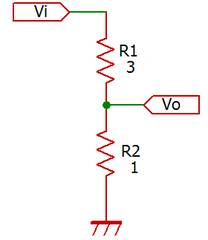
この図は入力電圧Viを分圧し、より低い電圧Voを出力する回路です。
回路ではViという電圧信号が与えられ、Voという電圧信号を取り出しています。なおGNDを共通にするという約束の下、入出力共にGND接続を省略しています。おかげで回路表記が簡素になり、見やすくなりました。
電圧ViによりR1とR2に電流が流れます(電圧差がある2地点が接続されていれば通常電流が流れます)。今回のように、直列接続のときはR1+R2の抵抗が接続されていると見なせます。
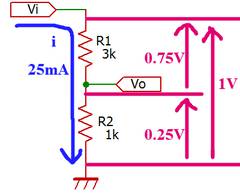
よってViを1Vとすればオームの法則から1V/(1k+3k)=25mAの電流iが流れます。同じくオームの法則からV=IRであるので、R1に25mA・3k=0.75V、R2に25mA・1k=0.25Vの電圧がかかります。電圧比と抵抗比が一緒になっていることを注意してください。
全体の電圧1VをR1とR2でそれぞれ分け合うので分圧といいます。Viが1Vのとき、Voは0.25Vになります。Viの1/4倍がVoとなり関係式で書くと次のようになります。
Vo = Vi/4
普通は抵抗分圧の一般式を示して終わるところですが、実のところ細かい式なんて覚えていませし、覚える必要もありません。
分圧の計算はまず電流を考えます。
i = Vi/(R1+R2)
得られた電流に求めたい部分の抵抗をかけます。
Vo = R2・Vi/(R1+R2) = R2/(R1+R2) ∵Vi=1
これで出力電圧が得られました。
並列な合成抵抗
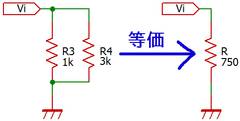
細かい式は覚えていないとは書きましたが、並列抵抗の合成抵抗値だけは覚えておいた方が良いです。
合成抵抗(値)とは複数の抵抗の接続を「あたかも1つの抵抗である」と見なしたの抵抗値のことです。合成抵抗を考えると複雑な回路も解析することができます。
R3とR4の並列抵抗値はR3//R4と書き、次式で求めることができます。
R = R3//R4 = (R3・R4)/(R3+R4)
代入すると、1k・3k/(1k+3k)=3k/4となり、0.75kΩになります。この式は「和(わ)ぶんの積(せき)」と覚えます。直列接続の場合は足すだけでしたが、並列だと多少ややこしいですね。
この式に色々な値を代入して計算すると、並列抵抗の特徴が見えてきます。
- 合成抵抗値は各抵抗値より小さくなる。
- 2つの抵抗値に差があるとき、小さい抵抗値の影響が支配的になる。
- 同じ抵抗値が2つ3つあるときは、合成抵抗値は1/2、1/3になる。
3つ以上の合成抵抗は3つのうち2つを合成し、合成した抵抗と残る1つを合成することで求められます。
合成抵抗にはちょっとした応用があります。どうしても91Ωの抵抗値が欲しいとき、100Ωの抵抗に1kΩの抵抗を並列につけると、合成抵抗が90.9Ωとなります。
また、この例からも分かるとおり小さい抵抗値の影響が支配的なので、10倍も違えば「小さいほうの抵抗値である」と見なしても多くの場合問題がなくなります。
出力抵抗と入力抵抗
電源を言えば何を思い浮かべるでしょうか。私はもっぱら電池を使用しますが、ACアダプタやSW(スイッチング)電源という人も多いでしょう。最近は減りましたがSW電源ではないACアダプタ(トランス電源)が昔は主流でした(有名なのはファミコンのACアダプタ)。
あるトランス式ACアダプタには12V500mAと書いてあります。これは12Vで500mAまで電流が流せるという意味……ではありません。500mA流したときに12Vの電圧になるよという意味です。100mAぐらいしか流さなければ14~15Vぐらいの電圧が出ます。不良品でも何でもなくこれが普通のことでした。しかし、電源なのに電圧が変わってしまう。これはどういうことなのでしょうか。
右図は、先ほど分圧のところで示した回路図の抵抗値を1/1000にしたものです。
この回路に1.5Vの単3マンガン電池を繋いでみましょう。分圧は1/4ですから、1.5/4 =0.375V=375mVが出力されるはずです。しかし実際に計測すると不思議なことが起こります。


計算上、1.412/4.3=328mVとなるべきものが238mVしかないのです。一体、何が起きているのでしょうか。
オームの法則が正しくないのではありません。オームの法則は正しく成り立っています。この謎の正体は電池にあります。回路を接続したまま電池電圧を測ると951mVと表示されました。238mVの4倍です(正確に4.3倍でないのは抵抗値誤差です)。電池から回路を切り離すと今度は1.412Vになります。
常に同じ電圧を出力する理想的な電源は世の中に存在しません。電源は必ず内部に抵抗を持ち、それを内部抵抗と言います。
内部抵抗を理解するために、電源を等価回路に置き換えます。等価回路とは理想的ではない素子を「実体に即して分かりやすく表した回路」のことです。
電源装置の等価回路は、理想的な電源*1と直列につながった出力抵抗roで表されます。
マンガン電池の内部抵抗(出力抵抗)は数Ωと言われますが、ro=2Ω, R1=3Ω, R2=1Ωとすれば、Vi=1.4・4/6=0.93Vとなり測定結果に一致します。このように内部抵抗が大きいと、大きな電流が取り出せません。
SW電源や直流安定化電源ならば内部抵抗はほぼ0と見なせますし、アルカリ電池の内部抵抗は0.数Ωと小さめで大きな電流が取り出せますが、一方で配線やコネクタ、電池バネ等が抵抗(~1Ω)を持つことに注意してください。電力を消費するR1やR2から見れば、配線抵抗も内部抵抗に見えます。
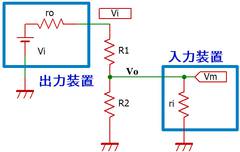
電源に限らず、すべての出力装置は「出力抵抗」を持ちます*2。これは電源Viを信号源の1つと見ることで理解できます。実際、電源も出力装置の1つに過ぎません。
入力抵抗について考えてみます。Voの先に電圧計など「何かしらの入力装置」が接続されているとして、等価回路に置き換えることができます。
例えば安いテスターなどではレンジによって入力抵抗が十分に高くないことがあります。Vi=1V, ro=0, R1=30k, R2=10kのとき、入力抵抗 ri=30kならば、Vo(=Vm)とGND間の抵抗値はR2//ri=(30・10)/(30+10)k=7.5k。計測電圧はVm=7.5/(30+7.5)=0.2V(本来なら0.25V)となります。
信号(電圧)を正しく伝えるためには、出力抵抗が接続先入力抵抗に対して十分に小さい必要があります。通常は10倍以上あれば問題ありませんが、高精度な測定をする場合は100~1000倍以上が必要になることもあります。例えばオシロスコープでは入力抵抗として10MΩか1MΩを使用するのが一般的です。*3
コラム4 ~出力抵抗を測る~
オームの法則を使って出力抵抗を測ることができます。まず何も接続しないで電圧を測ります。これが内部抵抗を無視したときの電圧になります(入力抵抗が十分大きいと内部抵抗を無視できる)。次に10Ωの抵抗を接続して電圧Vを測ります。すると抵抗に流れる電流iが分かり、同時に低下した電圧Vbが計測され、ここからroにかかる電圧Va=(V-Vb)が分かり、iとVaからroが求められます。
交流回路とコンデンサ
フィルタといえばコンデンサとコイルですが、無線回路以外ではコイルはあまり使われないのでコンデンサに絞って解説します。*4
コンデンサ(キャパシタとも言う)の特徴は、周波数によって抵抗値(に相当するもの)がころころ変化することです。
コンデンサCの抵抗値に相当するリアクタンス(単位Ω)は次式で求められます。
XC = 1/(2πfC)
「にーぱいえふしー分のいち」と覚えます。fは周波数です。
ちなみにコイルLのリアクタンスは
XL = 2πfL
です(同じく「にーぱいえふえる」)。リアクタンスはコンデンサとコイルの抵抗値に相当するもので、単位は共にΩです。リアクタンスとレジスタンス(抵抗)を区別せず呼ぶときはインピーダンスと言います。
とりあえずコイルのことは忘れ*4、1uFコンデンサのインピーダンスを求めてみましょう。
XC = 1/(2πf・1・10-6)
周波数fがあるので、それぞれ周波数別にインピーダンスを求めてみます。式から周波数に反比例することはすぐに分かります。
| 周波数 | 式 | XC |
|---|---|---|
| 10Hz | 1/(2π・10・10-6) | 16kΩ |
| 50Hz | 1/(2π・50・10-6) | 3kΩ |
| 100Hz | 1/(2π・100・10-6) | 1.6kΩ |
| 1kHz | 1/(2π・1000・10-6) | 160Ω |
| 2kHz | 1/(2π・2000・10-6) | 80Ω |
| 5kHz | 1/(2π・5000・10-6) | 30Ω |
| 10kHz | 1/(2π・10000・10-6) | 16Ω |
| 20kHz | 1/(2π・20000・10-6) | 8Ω |
関数電卓等がある人は実際に計算してみてください(この手の計算するとき関数電卓やポケコンは必須アイテムです)。電卓がなければ単純に2πを6と置いて手計算+電卓でも出せるでしょう。
直流は0Hzと考えることができ、このときコンデンサのインピーダンスは無限大です。直流成分を流さないというコンデンサの大きな特徴はこの式からも見て取れます。
簡単なハイパスフィルタ
やっとフィルタの話に到達できました。フィルタにはローパスフィルタとハイパスフィルタの2種類があります。ある周波数より低い信号(ロー)を通過させる(パス)フィルタがローパスフィルタ(LPF)で、ある周波数より高い信号(ハイ)を通過させる(パス)フィルタがハイパスフィルタ(HPF)です。
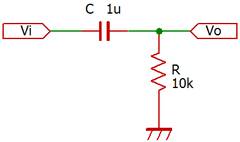
次の回路はHPFの例です。
| 周波数 | XC | 式 | 倍率 |
|---|---|---|---|
| 10Hz | 16kΩ | 10k/(16k+10k) | 0.38 |
| 50Hz | 3kΩ | 10k/(3k+10k) | 0.77 |
| 100Hz | 1.6kΩ | 10k/(1.6k+10k) | 0.86 |
| 1kHz | 160Ω | 10k/(160+10k) | 0.98 |
| 10kHz | 16Ω | 10k/(16+10k) | 0.998 |
この回路はずっと前に出た、抵抗の分圧と同じように考えることができます。
Vo=Vi・10k/(XC+R)
※この式は厳密には正しくありません。
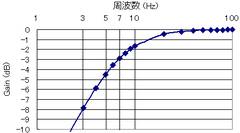
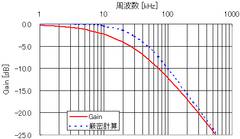
この結果をグラフにしてみます。Excel等で簡単に計算することができます。
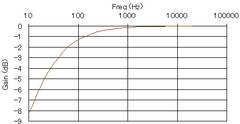
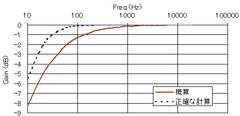
左図で1kHz以上ではほとんどの信号を通しますが、100Hz以下では減衰が大きいことが分かります。20Hz付近で-6dB(1/2倍の意味)となり、20Hz付近で信号が約半分になっていることが分かります。
右図は厳密な式に従って計算したグラフを示します。この差を大きいと見るか小さいと見るかは人それぞれですが、この程度の誤差があることを知っていれば概算で大雑把な傾向をつかむことができます。
(コラム)正確なコンデンサの計算
コンデンサを正確に計算するには、コンデンサのインピーダンスを-jXCとして計算する必要があります。jは虚数単位です。虚数は一般的にiを使用しますが、回路においては電流iと混同しないようにjを使う約束になっています。よってLPFの式は、
ゲインg = 10k/(-jXC+R)
となります。複素数は複素数のまま計算し、最後に有理化してg = A+jBの形にします。この複素数gの大きさがゲイン、偏角が位相になります。
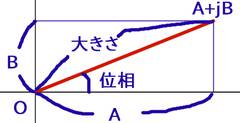
コイルの場合は jXLになります。この話を続けるとキリがないのでまたの機会に。工業高校向けの電気回路の教科書や参考書が分かりやすくお勧めです。ちなみに数学の教養があれば、よりスマートに解説できますが、身の回りのエンジニアはみんな数学が苦手だったりする不思議です。
dB表記の必要性
回路において、倍率はdB(デシベル)で表記するという習慣があります。倍率gを常用対数log10により次式で変換します。
G = 20log(g)
logは感覚量とも言われ、地震のマグニチュード等にも使われています。音で言えば、電圧を倍にしても人間には「倍の大きさ」とは感じられず、対数表記の方が人間の感覚に近いと感じられます。
dBには利点があります。それは計算がしやすいということです。dBが対数であるため、積算の代わりに足し算で済むからです。
例えば次のような回路の全体のゲインがいくつか考えます。普通に考えれば
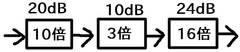
g = 10・3・16 = 480
となりますが、dB計算ならば
G = 20+10+24 = 54dB
となります。これなら暗算でもできますね。
| dB表記 | 倍率 |
|---|---|
| 6dB | 2倍 |
| 20dB | 10倍 |
しかしdBでは大きさがよく分からないという声もありそうです。これもコツを覚えれば簡単です。
左表の2つを覚えるだけです。
54dB = 20dB + 20dB + 20db – 6dB
ですから、10・10・10=1000倍より2倍少ない値となるので、約500倍とすぐに求められます。
フィルタ設計の実際
最後にフィルタをどのように考えて設計するかという話をして終わりたいと思います。今までの応用編となっていますので、挑戦気分で読んで頂ければなと思います。
カップリングコンデンサの検討
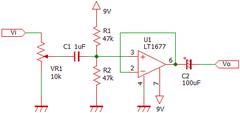
よくあるオペアンプ一発のアンプ回路です。9V電池1つでヘッドホンを接続し実際に動作させることができます。U1と書かれた三角形がオペアンプの記号です。オペアンプの解説は他に譲りますが、この回路では+端子側の電圧がそのまま6と書かれた出力から出てきます。「・」の打たれてない場所は交差していても接続されていません。回路図のルールですのでよく覚えておきましょう(ただし、うっかり打ち忘れた回路図もよく見かけます)。
C1、C2はカップリングコンデンサと言われます。DC(直流成分)を通さず音信号である交流信号だけを通過させるために使用されます。これらは低い周波数を通さず高い周波数を通過させるハイパスフィルタの一種です。C1、C2がないと出力や入力側に4V以上の直流が漏れ出してしまい問題があります。
入力側から見ていきます。信号の立場で考えるとき電源は0Ωの抵抗とみなし、プラスとマイナスは0Ωで繋がっていると考えます。よってR1とR2はVi側から見れば並列につながっています。これを踏まえて入力部分を等価回路に書き直します。
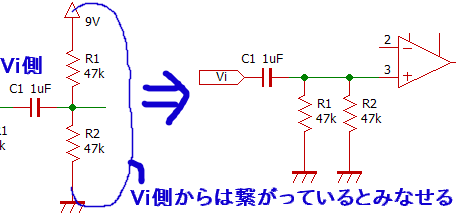
(補足)
R1とR2はバイアス回路と呼ばれます。オペアンプは電源電圧である0V~9Vより小さい範囲の信号しか出力できないため、-2V~2Vぐらいある音声信号を増幅することができません。R1とR2の真ん中の点は9/2=4.5Vであり、カップリングコンC1によって直流的な下駄を履かせています。これにより、-2V~2Vの信号は、カップリングコンデンサC1を経て2.5V~6.5Vの信号となりオペアンプ電源電圧範囲内に入ります。
R1とR2の並列合成抵抗値を求めます。同じ抵抗値の並列なので半分の23.5kΩです。よって1uFのコンデンサのうしろに23.5kの抵抗が1つ繋がっていると見なせます。
一番高いポイント(今回は1倍なので0dB)から-3dB(1/√2)下がるポイントをカットオフ周波数と言います。これを実際に求めてみましょう。コンデンサのインピーダンス
XC = 1/(2πfC)
が、抵抗値23.5kΩと等しくなるポイントが-3dB下がるポイントです。
23.5k = 1/(2πf・1u)
f = 1/(2π・1u・23.5k)
= 1/(2π・23.5・10-3) = 6.77Hz
6.7Hz付近が実際どのようなカーブになっているのかグラフを見てみましょう(厳密計算のグラフです)。
人間に聴こえる周波数は20Hz~20kHzであると言われ、HPFやLPFのカットオフポイントはこの外側に設定する必要があります。実際に20Hzの信号を完全に通過させたければカットオフのポイントを20Hzより低く設定することが望ましいです。例のように1/3のポイントだと、20Hzでほとんど減衰がありません。*5
入力部を設計したときの考え方を書いてみます。入力カップリングコンデンサに小さめのフィルムコンデンサを使いたいというのがまずあり、フィルムコンデンサでは1uF程度が限度ですので、そこからアンプ側の入力抵抗を決定しています。入力抵抗はノイズの面からできるだけ小さいほうが望ましく(かつ小さくてもVRの倍程度)、カットオフポイントの様子を見ながら20kΩ前後になるように設定しました。
(補足)
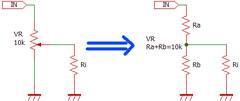
入力抵抗はボリュームの抵抗値よりも倍以上入力抵抗を高くしておく必要があります。ボリュームは分圧比を変えることで信号の大きさを変えています。
RbとRiは並列ですので、Riが例えば1kΩと小さければRbよりもRiの値が支配的となります。するとボリュームのカーブが狂います。別の見方をするとRiから見ればRa//Rbは信号(IN)の出力抵抗であるので、ボリュームの出力抵抗より十分高くなければならないのです。
続いて出力カップリングコンデンサを見てみましょう。
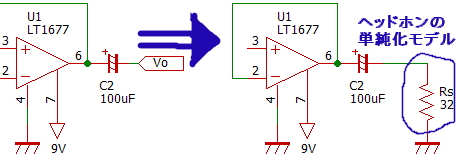
ヘッドホンはよく32Ωの抵抗をモデルとして使用しますが、この値はヘッドホンのインピーダンスに相当します。
試しに32Ωでカットオフを計算すると
32 = 1/(2πf・100u)
f= 1/(2π・100u・32)
= 1/(2π・3200・10-6) = 49Hz
となり、50Hz程度から減衰が始まるため20~50Hz程度の低音があまり出ないことが分かります。これはC2が小さすぎるためで、470uFに増やしてみます。
f= 1/(2π・470u・32)
= 1/(2π・470・32・10-6) = 10.58Hz
コンデンサの値を約5倍にしたので、通過周波数は約1/5になっています。カットオフ10Hz程度となり、満足な結果となりました。
ただし、ヘッドホンのインピーダンスは主なものでも16Ω~64Ω、他にも実に様々です。もし16Ωで同じ通過周波数を得るにはコンデンサを倍にする必要があります。
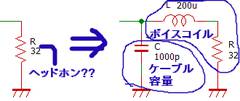
(コラム)~ヘッドホンのモデル~
回路設計上、ヘッドホンやスピーカーは「公称インピーダンス」相当の抵抗でモデル化されることが多いようですが、あまり適切ではありません。ヘッドホンは簡易なモデルでもコイルやコンデンサの組み合わせとして表すことになります(実際はもっと複雑)。
ヘッドホンやスピーカーは周波数によってインピーダンスが変化します。公称インピーダンスは、通常一番小さい周波数でのインピーダンスを示します。
ローパスフィルタコンデンサの検討
最後の回路はローパスフィルタ(LPF)を持つオペアンプ1発の低電圧アンプです。これも実際に動作します。
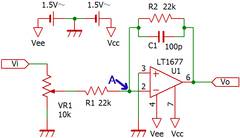
この回路はいわゆる反転アンプで、正負電源を使用したDC直結アンプにもなっています。DC直結アンプは、カップリングコンが無く、直流(DC)も増幅することからこのように呼ばれています。
この回路の増幅率gは次式で導かれます。
g = -R2/R1
R1=R2であるので、-1倍アンプです。マイナスというのが気になるかもしれませんが、要するに入力と同じ大きさの出力が出るアンプです。
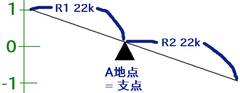
少々脱線しますが、A地点の電圧は+端子の電圧(この回路ではGND)と等しくなります。これはバーチャルショートと呼ばれる現象で、オペアンプの動作をイメージするのに役立ちます。
A地点の電圧は常に0であるので、動かない支点と見なせます。R1とR2はシーソーを構成していて(オペアンプの性質から同じ電流が流れるためシーソーと見なせる)、ここから入力電圧と出力電圧のイメージが掴めます。R1が1kでR2が10kならば何倍になるかすぐイメージできますね。
さてLPFとして動作するのは、R2と並列についているコンデンサC1の役割によります。C1のインピーダンスは周波数によって変化し、C1とR2の並列合成インピーダンスも変化します。この合成抵抗値をR2の代わりに使用すれば増幅率が分かります。簡易計算で表にしてみます。
| 周波数 | XC | 合成 | Gain | 厳密計算 |
|---|---|---|---|---|
| 1kHz | 1.6M | 22kΩ | -0.1dB | 0.0dB |
| 10kHz | 159k | 19kΩ | -1.1dB | -0.1dB |
| 20kHz | 80k | 17kΩ | -2.1dB | -0.3dB |
| 30kHz | 53k | 15kΩ | -3.0dB | -0.6dB |
| 50kHz | 32k | 13kΩ | -4.6dB | -1.6dB |
| 100kHz | 16k | 9.2kΩ | -7.5dB | -4.6dB |
| 200kHz | 8.0k | 5.8kΩ | -12dB | -9.3dB |
| 500kHz | 3.2k | 2.7kΩ | -18dB | -16.9dB |
概算で10kHzぐらいから減衰することが分かります。正確な計算だと30kHzぐらいからの減衰と見て取れます。20kHz以下はほぼ平坦になっています。
このLPFは位相補償とも言われ、オペアンプの動作を安定させる役割があります。オペアンプが発振しやすい数MHz以上で30dB以上の減衰があり効果的に発振を防止します。
LPFと同じようにR2の抵抗値とC1の容量から-3dBの減衰点であるカットオフポイントを求められます。
10k = 1/(2πf・220p)
f = 1/(2π・220p・22k)
f = 1/(2π・220・22・10-9) = 72kHz
以上でフィルタの解説は終わりです。簡易計算はカーブが正しく出ませんが、傾向をつかむなら十分です。大切なのは厳密な計算より頭の中で傾向がイメージできるかどうかです。
本当は1度ぐらい複素数を使ってきちんと計算して欲しいという気持ちもあるのですが、今でしたらLTSpice等のツールを使用して周波数特性を表示させるのが一番効率が良いと思います。そういうツールを使用するにしても「回路動作のおよその傾向」をイメージできることは大切で、簡易計算は回路図を読み、回路を設計するときにとても役に立ちます。
頭の中で回路の動作をイメージできるかどうかで回路の理解は大きく変わります。とにかく最初はイメージをつかむことを重視して、その後で細かい式を追いかけるとすんなり頭に入ると思います。
おまけ(発展的内容)
今回の解析は定常状態と呼ばれるものに対する解析です。定常状態というのは信号が安定した状態を意味します。多くの回路は信号を入れ始めた瞬間や、信号がなくなった瞬間は特殊な動作をします。
世の中の多くの回路はこの定常状態だけで考えることができますが、定常状態しか考えないと理解できない回路や設計もたくさんあります。信号を厳密に扱い回路を適切に設計するには、瞬間瞬間をきちんと解析できる非定常状態の回路解析の技術が必要になります。
電磁気学をやったことある人なら、コイルやコンデンサの話を聞いたことがあると思います。コイルやコンデンサは微分要素や積分要素になります。この微分・積分を、ラプラス変換という特殊な操作によってかけ算とわり算の世界に持ってくることができ、ラプラス変換後のsにj2πfを代入することで回路解析の世界につながります。物理現象としての素子の動作と回路動作は深く繋がっていて、昔の人が苦労して「回路工学」という学問を発展させてくれたおかげで、今こうして(複素数とはいえ)単純なかけ算とわり算で回路の計算ができるようになっています。
途中で、出力信号Voを入力信号Viで割った式を示しましたが、この式を伝達関数と言います。簡単に言えば「倍率」を発展させたもので、この式は周波数特性(f特)のほか位相特性(複素数の偏角)を含んでいて、非定常状態における信号の特性を知ることができます。
以上分かりにくいところも多々あったかと思いますがこれで終りです。感想質問などありましたらどうぞ。