漸化式でsin波を高速に生成する方法

はてブ数 2008/06/04理工メモ

漸化式*1によりsin信号を生成する方法を紹介します。これにより、マイコンのような機器でも高速にsin信号を生成することができます。FPGA等にも容易に応用できます。少し工夫すると円も描けます。

※高精度の演算には使えません。

*1 : 基本演算のみの反復計算不要な式

特徴

  • 任意の周波数、任意のサンプリング周波数でsin波を生成できます。
  • 初期値のみ、あらかじめ計算しプログラムに埋め込むか、別の方法で計算する必要があります。
  • 2次のIIR型フィルタにより生成するため、時間が経つと計算誤差が累積します。

生成周波数／サンプリング周波数が整数ならば、誤差の累積は非常に小さくて済みますが、それだったらテーブルで良いような気もします（でもメモリの少ないマイコンなら多少は有利かな）。

生成アルゴリズム

至って簡単です。

変数解説
y[n]生成系列
f生成周波数[Hz]
kサンプリング周波数[sample/sec]
phi初期の位相
PI円周率 / 3.1415926535....

初期値計算。

y[0] = sin(phi);
y[1] = sin(phi + 2*PI*f/k);
ar1  = 2*cos(2*PI*f/k);

生成式(n>2)。

y[n] = ar1*y[n-1] - y[n-2];

誤差が累積します。float型でためしたところ、（パラメータにもよりますが）1000回の計算で0.00012程度、10000回の計算で0.0012程度の誤差が出ました。doubleで生成すれば相当低誤差で使えそうです。

もしfがkで割り切れるなら１周した段階で（予め計算してある）初期値に戻してあげる方が良いです。割り切れない場合は、（もしsinを計算可能な環境ならば）適当な回数を演算したところで初期値計算を再度行うと良いでしょう。

永遠に計算し続けると、誤差の累積により発散するか0に収束すると思われます。

サンプル

Excelファイル（xls）。

Cのソース。

#include <stdio.h>
#include <math.h>
#define PI 3.14159265358979323846

float ar1,yz1,yz2;
sin_init(float freq, float sps, float phi) {
	yz1 = sin(phi);
	yz2 = sin(phi+2*PI*freq/sps);
	ar1 = 2*cos(2*PI*freq/sps);
}
float sin_get() {
	float g;
	g   = yz1;
	yz1 = yz2;
	yz2 = ar1*yz1 - g;
	return g;
}
main() {
	sin_init(1000, 10000, 0);
	while(1)
		printf("%f\n", sin_get());
}

原理

2次IIRフィルタを振動させているだけです。Z平面上での極を単位円上に配置してパラメーターを算出しています。

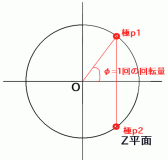
iir-sin01.gif
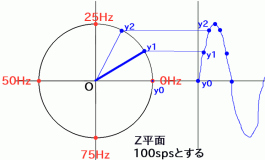
iir-sin02.gif

右の図に示すようにIIRによる振動現象は、単位円上を動く点と捉えることができます*2。きまった角度φずつ単位円の上をスライドする点を観測して生成されるものがsin波です*3。図で全体を100sample/secとして、各ポイントに対応する周波数を書きました。左に回転量が増えるほど周波数が高くなります*4。

IIRフィルタでの回転量を決めるのは、右図に示した「極」です。IIRフィルタで計算することは複素平面上で極を単純にかけ算することに等しいのです。複素数の授業でやったと思いますが、ある点に対して単位円上の点pをかけ算すると、その点は点pの角度だけ回転します。これが、IIRフィルタ（やFIRフィルタ、ARモデルやMAモデル）を貫く基本概念になります。

本当なら1次の極だけで足りるのですが、それですとIIRフィルタの係数が複素数になってややこしいので、一般には実軸対称の位置に（複素共役の位置に）もう1つ点を取ります。すると、2次の実パラメータを持つIIRフィルタが構成できます。

導出

フィルタの極p1は、周波数fとサンプリング周期kから次のように決まります。

p_1 = \cos(\phi) + j\sin(\phi) \qquad \phi = \frac{2 \pi f}{k}

もうひとつの極p2は実軸対称の位置に取りますから

p_2 = \cos(\phi) - j\sin(\phi)

です。極が２つあるときのIIRフィルタ伝達関数は

\begin{eqnarray} {\rm IIR}(z) &=& \frac{1}{(1-p_1z^{-1})(1-p_2z^{-1})} \nonumber \\ &=& \frac{1}{1-(p_1+p_2)z^{-1}+z^{-2}} \nonumber \\ &=& \frac{1}{1-(\cos(\phi) + j\sin(\phi) + \cos(\phi) - j\sin(\phi)) z^{-1}+z^{-2}} \nonumber \\ \therefore {\rm IIR}(z) &=& \frac{1}{1-2\cos(\phi)z^{-1}+z^{-2}} \end{eqnarray}

が導かれます。これをIIRフィルタの定義式に戻すと、

Y=2\cos(\phi)Yz^{-1} - Yz^{-2}

になり、アルゴリズムの式が導かれます。

*2 : インパルスのZ変換がy(0)=1になり、これはちょうど右を向いた(1,0)信号と思うことができますが、あとの話と整合性を取ろうとすると解説がややこしくなるので深入りは避けます

*3 : 余談になりますが、複素辺面上をスライドする点を実軸から捉えてcos、虚軸から捉えてsinと考えると、虚数平面上（２次元の平面上でも同じ）の点を捉える角度によって信号が異なるということがわかります。どんな観測信号も１次元に落とし込まれる（より正確に言えば射影される）段階で同じことが起きています。

*4 : この図でエイリアシングと呼ばれる現象を理解することができます。例えば75Hzの信号をスライドする点として順にプロットしてみると、左に270度ずつ回転させている(75Hz相当)にも関わらず、まるで右に90度ずつ回転している(25Hz相当)ように見えます。

注意

複数の波形合成を行ってその中から寄与率の低い波形の演算をやめるという手段を取ると、SONYの特許4019824に抵触する恐れがあります。まあ普通は触れようがないと思いますけど。

この特許、出願時（2002年）の資料を見るとsin波の生成だけで取ろうとした形跡がありますが、大昔から自明なこと（Z平面の単位円上に極を持つIIRフィルタは振動することと同値）なのでそりゃ無理です。